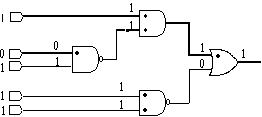
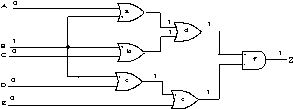
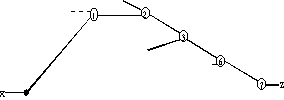
Figure 1. Example of CPT in a fanout-free circuit
Massoud Shadfar, Armita Paymandoust, and Zainalabedin Navabi
Electrical and Computer Engineering Department
Faculty of Engineering, Campus No. 2
University of Tehran
14399, Tehran IRAN
Tel: +98-21-800-8485; Fax: +98-21-688690
Email: navabi_z@irearn.bitnet
This paper presents a new method of critical path tracing for fault simulation. The details of this method, called one-pass critical path tracing, and its implementation in VHDL will be presented here. One-pass CPT is achieved by use of VHDL models for basic logical gates. By communicating via their ports, gate models a netlist will report faults that are detected on their ports due to application of test vectors at their primary inputs.
A method of fault simulation is critical path tracing. In this method a test is applied to a circuit and detected faults are reported. This is opposite to the fault simulation in which a fault is inserted in the circuit and various tests are applied until one is found to detect the fault. While critical path tracing (CPT) is very useful for test grading, it cannot be used for fault dictionary generation.
After applying a test vector, the present CPT methods find a critical path that leads to the output of the circuit, and declare faults on this path as detected by the test vector. Fanout stems are only marked as critical when values assigned to the stems are found to influence the output. This is done by partitioning the circuit and performing simulations on sub-sections of the circuit. Obviously this process requires a preprocessing of the circuit as well as iterative evaluation of node values by use of simulation.
We eliminate the required preprocessing and iterative simulations of CPT methods in a new CPT method called, One-Pass CPT. After propagation of values corresponding to a test vector, all critical values will be determined by evaluation of the circuit in one pass from the output to the input of the circuit. In this one pass, enough information will be accumulated and passed between various circuit components such that each component can independently decide on critical values of its inputs or driving lines.
An efficient environment for the implementation of One-Pass CPT is one of a concurrent language. Because VHDL is a hardware description language capable of representing netlists and also being a language for concurrent programming, it can be used in the implementation of one-pass critical path tracing. The implementation is done by writing special CPT gate models and resolution functions for fanouts. To perform critical path analysis on a gate level circuit, a regular VHDL component instantiation list must be bound to the CPT VHDL gate models. Test vectors applied to models of this circuit will cause the models to report detected faults due to the application of the test. This work will be useful in integrating test related processes with present VHDL based simulation and synthesis processes. This will move VHDL in the direction of a language for all design and test applications.
This paper presents an overview of fault simulation in Section 2. In Section 3, the details of the one-path CPT will be discussed. Based on the discussion of Section 3, the VHDL implementation of one-pass CPT will be discussed in Section 4. An environment that uses these models will be presented in Section 5. In this section a simple example and the list of detected faults reported by CPT models will be discussed.
In the area of digital system test fault simulation plays an important role in test generation, test grading, creation of fault dictionaries, etc. Because fault simulation must evaluate a circuit for many possible faults, fault simulation of large circuits with thousands of gates becomes inefficient. Approximate methods such as critical path tracing [1, 2, 3] and statistical fault simulation [4, 5] can be used as alternative to fault simulation for special applications such as test grading and test evaluation. With their limited application, such methods improve speed. Critical path tracing is based on true value simulation and does not require specific fault insertion.
2.1 CRITICAL PATH TRACING
In fault simulation by critical path tracing, specific faults are not specified. In order to find faults detected by a certain test vector, the test is applied to the inputs of the fault free circuit. This vector determines all intermediate circuit logic values. If a line value is forced to its complementary value, and this value causes the output of the circuit to toggle, then we can conclude that a fault on the line with the new complementary value can be detected at the output. Such line is said to be a critical line of the circuit with the applied test. Finding critical lines becomes more involved in circuits with re-convergent fanouts. To provide necessary background for describing our critical path tracing, an example with and without fanout will be presented.
Figure 1 shows a fanout free circuit. The 10111 test at the input of this circuit causes the output value to become 1. Since changing the upper input of the OR gate changes the output value, the line at this input is critical for the applied test vector. Obviously, since the lower input line is not critical, no line that leads to this line is critical. On the other hand, lines leading to the upper input of the OR gate can still be critical. Applying the arguments used with OR gate to the other gates of the circuit, results in critical lines as highlighted in the circuit of Figure 1.
Figure 1. Example of CPT in a fanout-free circuit
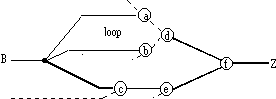
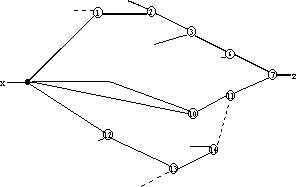
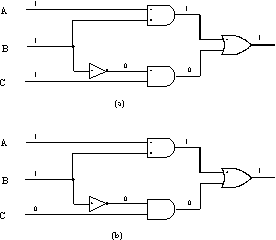Figure 2. Critical path tracing, with re-convergent fanout
2.2 CPT METHOD
In the original critical path tracing method [1], primary input values are propagated to all circuit lines. The circuit is traced from output to input for identifying critical lines in a manner similar to what was described in the previous section. In the process of this tracing, when a fanout is encountered, a simulation phase will determine if the effect of changing the value of a fanout stem will be marked as critical. In order to reduce the size of the part of the circuit that is simulated, a partitioning of the circuit is done to simulate only up to the point whose effect on the output is known.
From the above discussion it is clear that critical path tracing by this method requires much forward simulation and backward propagation in an iterative fashion. In addition, partitioning of the circuit into isolated parts with inputs influenced by fanout stem and outputs influencing the primary output is a time consuming process.
Above all, the case mentioned at the end of the previous section in which a fanout stem can be critical even if none of its branches are critical, cannot be handled by the standard CPT method. This is because, the method requires a critical path through branches to reach to a fanout.
Considering the problems associated with the original critical path tracing algorithm, we have developed a new method that eliminates the need for any partitioning or partial simulation of the circuit. In one pass CPT, simulation is only necessary at the beginning when a test vector is applied. Decision to mark a stem as critical will be based on the information that is passed from gates that are driven by the fanout branches back to the fanout node. In general one pass CPT is centered around the facts that 1) A gate with critical output locally decides on its input lines being critical, and 2) Fanout stems require information from all their branches before they can declare a stem as being critical. Therefore gates, interconnecting lines and fanout nodes must cooperate in providing necessary information to gates and fanout nodes.
3.1 GATE BEHAVIOR
Based on the type and the output value of a gate, a gate makes certain decisions about its input lines. A gate may declare an input line as being critical or it may declare an input as being blocked from becoming critical by another one of its inputs. The expected behavior of a gate is to identify each of its inputs as being critical or being blocked. In a two input AND gate, shown in Figure 3, if only one of the inputs of the gate has a controlling value (Figure 3-a) that input line is critical and the other is blocked, from being critical. If both inputs of a two input gate have controlling values, Figure 3-b, then each input is considered as blocked by the other input. Therefore, both inputs will be refereed to being as blocked. In this case if both inputs change simultaneously, the output value will toggle. As shown in Figure 3-c, if both inputs of a gate have non-controlling values then both inputs are critical, since changing each input will change the output value. The significance of a gate in one pass CPT is only due to its critical and blocked input lines. The notation shown in Figure 4 is a simple notation that eases our analysis of critical path tracing . Critical lines are shown by solid lines, while dotted lines represent blocked lines.
Figure 4. Gate notations
a) One critical and one blocked input
b) Two blocked inputs c) Two critical inputs.
An interconnection of several gates for critical path tracing can be done by use of a graph using the notation presented in section 3.1. Such a graph will be refereed to as critical path graph (CPG). Figure 5 shows a simple AND-OR circuit and its corresponding CPG.
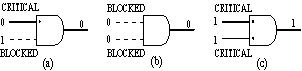
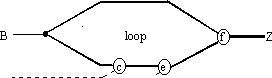
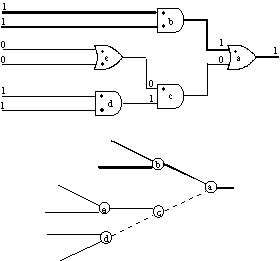Figure 5. Critical path graph
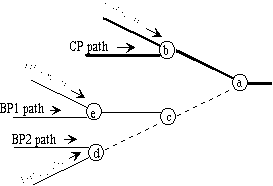Figure 6. Path kinds
In addition to gates determining the kind of their input lines, the other decision made in one pass critical path tracing is the decision to mark a fault stem as being critical to not critical. This decision is made by a fanout node and will be based on the types of paths (CP and BPn) associated with fanout branches. The following definition is needed for study of fanout behavior.
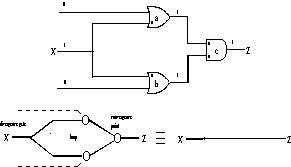Figure 7. Rule a replaces two converging critical paths
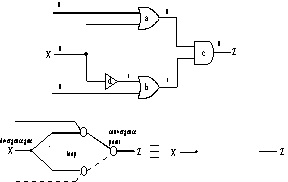Figure 8. Rule b removes a converging CP and BP
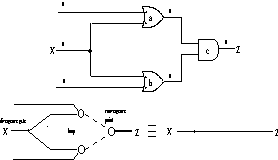Figure 9. Rule c replaces two converging Bps with a CP
(a)
(b)
Figure 10. Applying Rules a,b, c, and d
(a)
(b)
Figure 11. Continuing example of Figure 10
(a)
(b)
(c)
Figure 12. A complete example
The above rules and their application to logic circuits can be easily implemented in a concurrent programming environment. The above discussion facilitates the presentation of VHDL gate models for performing critical path tracing.
After the initial simulation, and after several delta times, all node values will be known. Based on its output values each gate produces CP or BP on its inputs. Primary outputs, being always on a critical path, initiate critical value determination of the output gates. Therefore gate models may observe a CP transaction on their outputs. Such a gate will decide CP or BP on its inputs. This information will eventually be collected and observed at a fanout node. In order to keep track of paths leading to a fanout, each gate collectively send its identification along with the kind information (Critical or Blocked) on its input line signals.
Faults detected are reported by the individual gates and PIs, and POs. Fault detected at a fanout stem will be reported by gates or PIs immediately connected to it. The VHDL implementation of critical path tracing consists of types, resolution function, gate models and utility programs. In this section each of these parts will be described. Before this description, we will make definitions for relating rules of Section 3 to the VHDL coding.
4.1 INFORMATION FIELDS
Interconnecting lines between gates carry information in the forward and backward directions. In the forward direction only logic values are transmitted. In the backward direction information regarding critical, blocked, and the index n number of blocked paths (CP, BPn) are transmitted. The logical values will be referred to as logic, and the information needed for critical path algorithm will be referred to as path_info.
4.2 CRITICAL LEVELS
Path_info of a node whose forward logical value is not known (U) is none. The code value for this state is -3. At the beginning simulation all line path_info is none. After an input vector is applied to the primary inputs, logic values propagate to the outputs changing logic values to '0' or '1', while keeping path_info values to none. The process of determining path_info begins with outputs identifying themselves as critical (CP). CP is a value that is assigned to the path_info and has a code value of 0. Path_info propagate backwards from output towards the inputs of the circuit. On their way, all lines will receive different values of path_info. If an input of a gate is blocking critical path of another input, its path_info becomes BP1 which has a code value of 1. A BPn blocked by another input becomes BPn+1, increasing its code value by 1.
The level of a path_info is determined by its code value. Therefore, CP with level 0 has the lowest level and a BP5 with level 5 has the highest level. Two adjacent levels are those whose codes are consecutive numbers of 0, or above (i.,e., none is not included).
If a line is neither critical nor it is blocking a critical path, it is UNCP and has a code value of negative 2. A similar line, but one that also contains fanout stem information has a code of -1 and will be referred to as UNCP_I.
4.3 LINE TYPE
A line type for containing logical and path information is shown in Figure 13. This is a record named fsim with logic and path_info elements.
TYPE fsim IS RECORD logic : imp; path_info : bkt; END RECORD; |
The path_info element is an array of 4 rows and 20 columns of integers. Path information on each line is included in this array. In each row, the first integer specifies a code value of a path. Therefore a line that is part of a critical path has a 0 value in position (0,0) of the path_info array. The rest of the integers in a row of this array contain gate identifications for all gates that a critical path has gone through. The other three rows contain similar information which will be described in the following sections.
The path_info element of the fsim record is resolved by the backtracing resolution function (bkt). For non fanout nodes, the role of this function is to pass path information from an input of a gate to output of another. For fanout nodes this function will make decisions regarding passing of path information to fanout stems. The details of this function will be described in a later section.
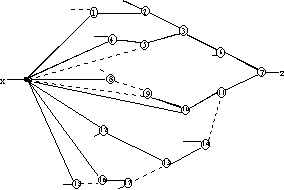
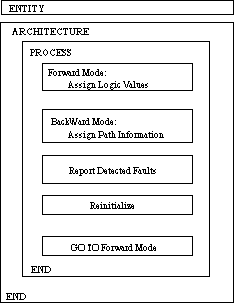Figure 14. General CPT model structure
A gate model has inputs and outputs of type fsim and INOUT mode. A model is responsible for forward propagation of logic values, and backward (output to input) propagation of path information. A model is also responsible for reporting its inputs and outputs on which faults are being detected. Each gate has a unique identification number passed to it via a generic clause. A single process in the statement part of a gate architecture handles logical and path information generation. In the following discussion we will use a two input NAND gate for demonstrating the behavior of critical path tracing models. A general outline of a gate model is shown in Figure 14.
4.4.1 LOGIC OPERATION
The code for generation of logic value on the output of a gate is shown in Figure 15. After none 'U' values are observed on all gate inputs, a gate uses logic field of its inputs and assigns proper value to the logic field of its output. At this time the gate goes in the backward mode and will only be sensitive to events on the path_info field of its output. When fault values for specific test vector have been reported by the individual gates, gates will again go into forward mode and again become sensitive to events on their inputs. The process of re-initialization which operates after a gate has reported its detected faults is shown in Figure 16.
............ WAIT UNTIL i1.logic /= 'U' AND i2.logic /= 'U'; in1 := i1.logic; in2 := i2.logic; out1 := in1 NAND in2; o.logic <= out1; .............. |
............ --- initialization i1 <= none_U; i2 <= none_U; o <= none_U; --- wait until all lines in circuit initialized. WAIT FOR 10 PS; tn := tn + 1; ........ |
A gate waits until an event on its output changes path_info field of the output to a value other than none. This happens when a code value greater than -1 is placed on the path_info of an output. The code value of a path_info greater than -1 is an indication that the output is either on a critical (CP), or it on a blocked path (BPn). In this case, based on input logic values, path information for the path_info fields of the inputs will be determined and assigned to the fields of the individual inputs. The code section responsible for this behavior is shown in Figure 17.
......... ELSIF temp_o(1,1) > -1 THEN IF in1 = '0' AND in2 = '1' THEN temp_i1 := added_node(temp_o,id); temp_i2 := increment_depth(temp_o,id); ELSIF in1 = '1' AND in2 = '0' THEN temp_i1 := increment_depth(temp_o,id); temp_i2 := added_node(temp_o,id); ELSIF in1 = '0' AND in2 = '0' THEN temp_i1 := increment_depth(temp_o,id); temp_i2 := temp_i1; ELSE .......... |
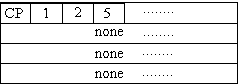Figure 18. A path information example
Assignment of values to path_info of inputs when they are '1' or '0' is done similarly. For in1, in2 being '00' increment_depth procedure is called for both inputs since each input is being blocked by the other input. For in1, in2 being '11' added_node function, which appends the current gate id to the output path_info while preserving the code value of the output, is called for both inputs.
IF temp_o(1,1) = -1 THEN IF in1 = '1' AND in2 = '0' THEN temp_i1 := uncp; temp_i2 := temp_o; ELSIF in1 = '0' AND in2 = '1' THEN temp_i1 := temp_o; temp_i2 := uncp; ELSIF in1 = '0' AND in2 = '0' THEN temp_i1 := uncp; temp_i2 := uncp; ELSE temp_i1 := temp_o; temp_i2 := temp_o; END IF; |
4.5 PATH INFORMATION EXAMPLE
The circuit of Figure 21 shows path information on various lines of an AND-OR circuit. Since gate 1 in this figure is a PO, its output is CP. The path_info placed by this gate on its input contains its id and code value 0 (for CP). Gates 2, 3, 4, and 5 each append their id to the path_info at their output and assign it to their '0' logic value input
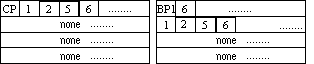
s. This happens because value of '01' on inputs of an AND gate makes the '0' input critical.
The lower input of gate 2 is being blocked by the upper input. Therefore, the path information on this gate includes the critical path of its output plus an indication that this path is being blocked once at gate 2. Since the lower input of gate 6 is on a critical path with respect to its own output, therefore, the path_info on this input consists of the path information on the output with gate 6 id appended to its first row. On the other hand, since the lower input of gate 7 is being blocked, blockage level is increased by 1 (changing BP1 to BP2) and the blockage information on the output of this gate is copied to the second row of the input path information.
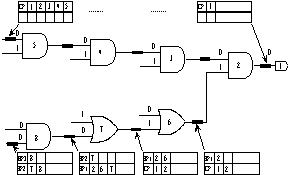Figure 21. Path information for a simple AND-OR circuit
Although, all interconnecting lines are resolved, resolution of value is only significant at the fanout nodes, and that is only important when processing path information in the backward direction. The resolution function for this purpose is called backtracing which will be discussed here.
Drivers of the backtracing resolution function are path_info that reach a fanout from various gates. The resolution function makes a copy of all its drivers in a temporary buffer and starts processing and making modifications to this buffer using rules a, b, c of Section 3.
FUNCTION backtracing (paths : int_4by20_vector) RETURN int_4by20 IS VARIABLE temp1, temp2 : int_4by20_vector(paths'RANGE); VARIABLE depth, util1 : INTEGER := 0; VARIABLE util2, connection : BOOLEAN := false; VARIABLE num : INTEGER := INTEGER'HIGH; VARIABLE rejector : int_4by20 := rjct; VARIABLE constructed, agent : int_4by20 := none; VARIABLE select1, select2 : INTEGER := -1; |
FOR i IN paths'RANGE LOOP -------- deepest path will be found. IF depth < temp1(i)(1,1) THEN depth := temp1(i)(1,1); END IF; END LOOP; |
......................
IF depth > 0 THEN ------------- construct and reject
FOR i IN depth DOWNTO 1 LOOP
-- path with i depth will be constructed.
FOR j IN paths'RANGE LOOP
IF temp1(j)(1,1) = i THEN
FOR l IN j + 1 TO (paths'LENGTH - 1) LOOP
IF temp1(l)(1,1) = i THEN
replace_check (
temp1(j), temp1(l), constructed, connection);
IF connection THEN
temp1(j) := constructed;
temp1(l) := none;
END IF;
END IF;
END LOOP;
END IF;
END LOOP;
FOR j IN paths'RANGE LOOP
---- path with i-1 depth is rejected
IF temp1(j)(1,1) = i THEN -- by path with i depth.
FOR l IN paths'RANGE LOOP
IF temp1(l)(1,1) = (i - 1) THEN
remove_check (
temp1(j), temp1(l), constructed, connection);
IF connection THEN
temp1(l) := constructed;
END IF;
END IF;
END LOOP;
END IF;
END LOOP;
END LOOP;
END IF;
........
|
After application of rules a and c, as above, the resolution function searches the temporary buffer for remaining BPn path_info that have not been replaced by BPn-1. In this case, if a BPn-1 is found that has a common node at the convergence point with the BPn under consideration, then the two path_info will be removed from the temporary buffer. This removal process is done by performing rules b and d, which are checked by the remove_1_check function.
The above processes, in which rules a, c and b, d are applied, will be repeated for all path_info from highest to the lowest blocked level (BP1). When this is done, if the resulting path_info in the temporary buffer has level 0 (CP), then the fanout stem is critical, otherwise the fanout stem will be declared as being un-critical (UNCP_I).
The critical path analysis models can be used for non-deterministic test generation of for fault simulation. Because the netlist is a standard VHDL instantiation list, the same netlist can be used for other test activities such as VHDL based test generation or fault list generation [8,9]. In this section we will demonstrate the use of our models for fault simulation through the use of an example.
...... PI3 : pi GENERIC MAP(3) PORT MAP(S(3)); PI4 : pi GENERIC MAP(4) PORT MAP(S(4)); G8 : or2 GENERIC MAP(9) PORT MAP(S(6),S(4),S(7)); G9 : or2 GENERIC MAP(10) PORT MAP(S(9),S(8),S(10)); G10 : not1 GENERIC MAP(11) PORT MAP(S(10),S(11)); ...... |
TEST:GATE(ID) *****DETECTED SSF***** ] ...... .............................. 1:OR2 ( 9) [I1:sa_0; I2:none; O1:sa_0 ] 1:OR2 (10) [I1:none; I2:none; O1:sa_0 ] 1:NOT (11) [I :sa_0; O :sa_1 ] 1: PO (12) [PO:sa_1; ] 2: PI ( 1) [PI:sa_1; ] 2: PI ( 4) [PI:sa_1; ] ........................................ |
In this paper, we have presented a new method of critical path tracing for fault simulation. This method is called one-pass CPT and it performs critical path tracing in only one output-to-input pass. We avoid circuit partitioning and incremental simulation of the circuit. Rule c detects critical stems that are not detected by the present CPT methods. We have implemented the one-pass CPT in VHDL. This language is specially appropriate because of its ability to model concurrent processes. We have developed other VHDL based test related tools such as test generation and fault collapsing. The combination of such models used in a test environment can provide necessary test tools for hardware designers using the VHDL language based tools in their designs. The models presented here suggest a new test methodology as well as new application for the VHDL language. Although, results have been verified with use of conventional methods, performance comparison is not relevant at this point.